In this article, we will compare and explain the most common list and set operation in Python. We will cover the advantages of using set and table with examples.
Why would you use a set?
Python offers set operations like:
intersection- get elements from list1 and list2union- return all unique elements from both listsunion all- all unique elements from both lists with repetitionsubtraction/difference- elements from list1 not in list2symmetric_difference- return a new set with elements in either the set or other but not both.
Sets also provide built-in methods for performing these operations. In some cases you may need to expand their behaviour.
Set vs List in python
In Python
listis an ordered collection of elements that can contain duplicates- allow duplicates
- mutable
- add / remove elements
setis an unordered collection of unique elements- unique elements
- mutable
- add / remove elements
- better performance
Both data structures have their own advantages and use cases.
Python list vs set performance
When it comes to performance, set have much better performance than lists. For certain operations like the in operator
set- has O(1) average time complexitylist- has O(n).
So checking if an element is present in a set is much faster than same check for a list.
Additionally, set operations such as:
unionintersectiondifference
also have better time complexity than their list counterparts.
Dealing with list with many elements then you need to use set to speed up your applications.
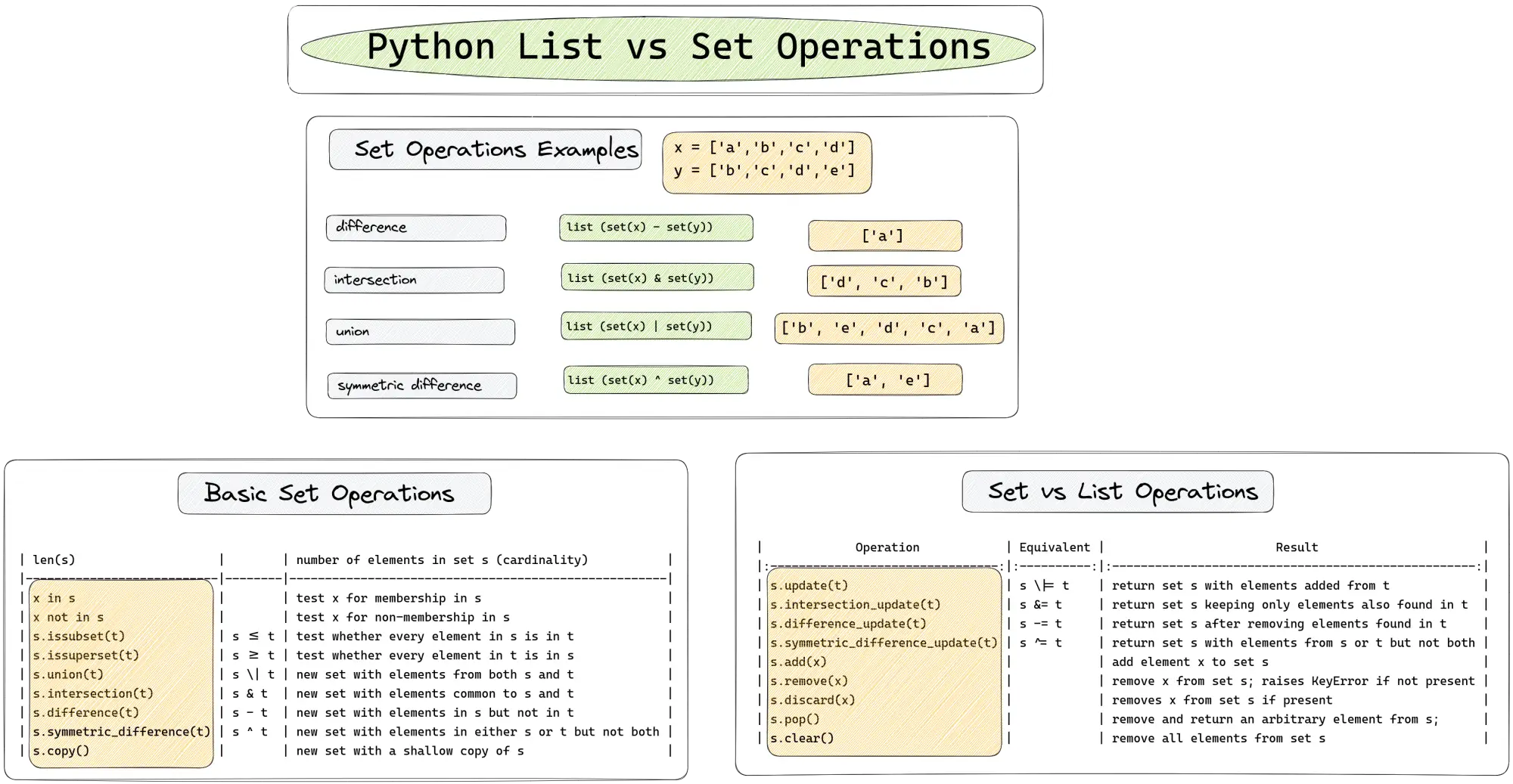
Set operations Examples
set gives you an easy way to find the difference or the intersection of two lists.
In the next code examples we can see most common set operations:
x = ['a','b','c','d']
y = ['b','c','d','e']
print (list (set(x) - set(y))) # difference
print (list (set(y) - set(x)))
print (list (set(x) & set(y))) # intersection
print (list (set(x) | set(y))) # union
print (list (set(x) ^ set(y))) # symmetric_difference
result:
x - y: ['a']
y - x: ['e']
x & y: ['d', 'c', 'b']
x | y: ['b', 'e', 'd', 'c', 'a']
x ^ y: ['a', 'e']
This example works with lists/sets from different sizes.
If you have interest take a look in this: Set Types — set, frozenset
Python set operations
Below you can find table about most common set operations:
Basic set operations
| Operation | Equivalent | Result |
|---|---|---|
| len(s) | number of elements in set s (cardinality) | |
| x in s | test x for membership in s | |
| x not in s | test x for non-membership in s | |
| s.issubset(t) | s <= t | test whether every element in s is in t |
| s.issuperset(t) | s >= t | test whether every element in t is in s |
| s.union(t) | s | t | new set with elements from both s and t |
| s.intersection(t) | s & t | new set with elements common to s and t |
| s.difference(t) | s - t | new set with elements in s but not in t |
| s.symmetric_difference(t) | s ^ t | new set with elements in either s or t but not both |
| s.copy() | new set with a shallow copy of s |
Python set operations on lists
| Operation | Equivalent | Result |
|---|---|---|
| s.update(t) | s |= t | return set s with elements added from t |
| s.intersection_update(t) | s &= t | return set s keeping only elements also found in t |
| s.difference_update(t) | s -= t | return set s after removing elements found in t |
| s.symmetric_difference_update(t) | s ^= t | return set s with elements from s or t but not both |
| s.add(x) | add element x to set s | |
| s.remove(x) | remove x from set s; raises
KeyError if not present |
|
| s.discard(x) | removes x from set s if present | |
| s.pop() | remove and return an arbitrary
element from s; raises
KeyError if empty |
|
| s.clear() | remove all elements from set s |